I thought Mark Bofill might enjoy this physics problem which was actually assigned to one of my students. I’m showing it exactly as presented to the student (though reduced in size.)
As a rather minor comment, I’d like to point out the image inserted is merely “decorative”. Nothing in the image clarifies the question (which is, btw, repeated both before and after the image). Also, I know from experience that some students view these questions on smallish screens (iPads.) The inclusion of the images means they read the question and then need to scroll down to the answer box. Now, one might say the need to scroll is a “first world problem”, but I would also suggest that inclusion of the image is both needless and, if anything, counter productive. But that’s just me.
Now for the bit that makes me think Mark Bofill will enjoy this. Recall previously after reading the text of a problem that appeared on the DuPage county Regional Office of Education physics tests, Mark commented:
This doesn’t really pertain directly, but it was nagging at me. The initial problem with the child accelerating the wagon would seem to require a child of unusual athletic talent. Kid needs to be in contact with the wagon for the three seconds to be applying the force, so at the end that kid is cooking along at 15 m/s too.
Adults don’t really sprint faster than 12 m/s.
Based on that thought he might enjoy the solution to this problem. I’m squinting, but the relevant part of the text appears to read:
“A boy throws a small bundle of flowers toward his girlfriend on a balcony 11.1 m above him. The bundle stopped rising after 2.61 s.
How high did the bundle travel?”
The answer to this is to first ‘know’ that a bundle of flowers should be modeled as an ideal projectile (i.e. no drag on the fluffy decorative fronds). Then recognize the bundle of flowers has zero velocity at the top of the trajectory, and know the distance traveled up is the same as the distance it would take for it to fall down from that height. In this case: H = 0.5* 9.8 m/s2 (2.41 s) 2.
The answer is: H = 33.37929 m. Which is 109 ft.
What speed did he through these at? Assuming he toss them straight upV= 9.8 m/s2 * 2.41 s 25.6 m/s ~ 52.832 mph.
I’m know professional baseball pitchers can throw 80 mph. But really… Romeo tossing a bundle of flowers at 57 mph? Which is fast enough to vault three times the height of the balcony? Thank heaven there really would be drag otherwise the minimum velocity when those flowers fall back down on Juliet is 20.9 m/s (46.7 mph.) She better dodge those and let them splat on the balcony!
FWIW: I actually grabbed a bunch of sedum with nice fluffy flower heads on it and tried to toss one straight up. I couldn’t get more than 12 feet. So I asked my burly neighbor. He maybe got 15-16 feet. We tried straight up, a bit of an angle and so on. We didn’t try to make a bundle and optimize the shape or weight to make the flowers more throw-able.
I have to admit I’ve written similarly unrealistic problems using Moodle’s random number generator. (I later learned to write an R script to attempt to avoid having roller coasters fall off their tracks at the top of the “loop-de-loop”, or kill passengers from excess ‘g’ forces.) But trying to write problems that meet all the rules of ‘optimum’ why I prefer to use “super ninja” when writing physics problems.

Of course Super Ninja will do things no mere mortal can do. But I can at least write problems where students don’t can minimize need for a calculator, reduce challenges of entering numerous digits in the ‘moodle’ entry box and so on. With Super Ninja, a student with a sense of what is physically plausible won’t hesitate over the answer because it violates their sense of what could even happen: after all, this is “super ninja”.
Did you ever wonder why there were so may problems with “Wiley Coyote” and “Road Runner”? I’m pretty sure this is why. Possibly the boy in question here is “super boy” who lives on “airless planet X” which looks just like earth and whose local acceleration due to gravity the student is supposed to just know. Or something.

🙂 I did enjoy that.
I’m glad I’m not the only one who does stuff like this.
Thanks Lucia!
:> Ah, the unintended, unforeseen consequences of ballistic romance. To be young again…
John Wheeler reported an exam question by a guy named Cooper. “How far can the wild goose fly?”
Mark Bofill,
Well… yes. And perhaps the follow on question presented during “impulse momentum” might be to find the average force exerted on Julliet’s head given some specified mass of the flower bundle and deceleration time δ t.
jferguson,
In one trip? I guess we could bound it in a variety of ways. Perhaps estimate how many excess calories the goose is stocked up on, estimate drag and distance. Once he’s burned up his excess calories the goose needs to land and refuel.
I’m not sure how else one would bound it. I don’t know the weight of a typical wild goose, nor how much of his body weight is excess calories. But perhaps there are courses where such a question is not unreasonable. It would seem a big challenging in high school physics– unless this sort of estimate had been discussed.
With respect to some questions, whether they are reasonable or not depends on content of a course.
Why isn’t the answer simply 9.8*(2.61^2) ? or 66.76 Meters?
What height? This would give height above release point from boy’s hand? (pedantry?)
How did you get from 2.61 seconds to 2.41 seconds?
Because there is a factor of 1/2 when you integrate x” the second time to get x.
Typo on the 2.41. It’s 2.61 in the question, but squinting I read as 2.41 at some point. Then I saw my error but clearly did not fix it thouroughly.
Oh… and yes, that is the height from the release point of the boy’s hand. As per usual, the principle of “read the problem to be asking for something that can be computed” is invoked. So, I assume the boys hand is at the ground (which makes no sense.) Clearly, if we estimate his height, knowing seconds two 3 significant figures is a bit much.
Lucia,
That wouldn’t have occurred to me, and yet once you point it out it’s obvious. Sort of disturbing actually, I wonder how often I sneak assumptions in like this when doing real work. I guess empirical testing is what saves us all at the end of the day from things like this.
The goose question was asked in an engine school course on estimating. it sounds like your on the right track.
Dad had a similar one semester course in EE at U of Minn in 1940 which included things like designing a clothes-washer to work on Mars.
hoping I’m not drifting the topic too much, i had a fascinating lunch with a guy whose job at the Torpedo Factory in Newport was to determine whether problems were soluble – and I think not just mathematically. Apparently this is a discipline and he had a PhD in it from Brown.
Mark Bofill:
Eh. It turns out the boy’s height was irrelevant so the assumption didn’t matter.
Brandon,
Really? I wouldn’t be surprised to be making a mistake. ( 🙂 Seriously, not at all! 🙂 ) But it seems pertinent to me:
Right, so he throws them. What does that mean? He holds them in his hand, accelerates his hand using his arm, and releases them. This happens at ground + what? A meter, a meter an a half, something like that. He releases the flowers, they’re traveling with some velocity and gravity is decelerating them, we know by the amount of time it takes for acceleration due to gravity to overcome the initial velocity everything we need to know — except, it seems to me, how high off the ground they were when they left the boy’s hand.
How high measured how? Off the ground or from the boy’s hand?
Probably happens at ground + 2.5 meters more like, the more I think about it.
The flowers travel 30+ meters. The balcony is only 11.1 meters above the boy. There’s no height or release point you could pick for him which would change the answer. Even if your assumption about his height changed the distance by 10 meters, the answer would still be the same.
Brandon,
I’m getting that distinct and disagreeable feeling that [edit: suggests] I’m being dense.
The answer, presumably to this question:
Ohhh. I think I’ve got you now. How high did the bundle travel.
Careful reading helps, if this is what you meant, thanks Brandon!
The question can’t be answered without a reference point. How high compared to what, the balcony, the ground, the boy’s head? In every case, you need to know the height of the release point.
Now if the question was how far did the bundle travel, the reference point is indeed irrelevant. But it wasn’t.
Edit: And even that assumes no horizontal velocity component at release, which seems unlikely given that the boy should be aiming for the flowers to land on the balcony and he can’t be standing directly below the balcony or the flowers would hit the bottom of the balcony on the way up.
When the specs are ambiguous, the customer gets what they gets and they don’t gets to pitch a fit about it. Don’t I wish…
Brandon,
Whether the question as asked means “how high relative to the launch point” or “how high relative to the ground” could be debated. The clause nailing down what “high” is relative to is not there and people of good will could read it either way. But to solve the problem, one must assume “relative to the boys hand”.
My estimates of the speed with which it hits the balcony assume the boy’s hand is at the ground. Otherwise, it’s hitting the balcony at a faster speed. (Also, it’s hitting at a faster speed if the flowers initially had some horizontal velocity.)
Lucia,
it sure looked to me like the balcony wasn’t involved. How high the flower went is the sole question.
jferguson,
There are actually two questions (but only one answer box.) Squint before and after the image. The “real” question is the first one. The box doesn’t accept “Yes” as a valid answer.
But with respect to the ambigiuity of the question: We can find many instances of actual honest to goodness people writing things like
“he has traveled as far as South America and Canada …”
You see more.
https://www.google.com/search?q=how+far+did+they+travel&ie=utf-8&oe=utf-8#q=%22traveled+as+far+as%22
While one might suggest that in physics, “travel” maps into “absolute value of displacement during problem under consideration” it’s not clear that “rule” makes 100% sense if one is simultaneously trying to ask “real world” questions in which one uses English phrases to mean what they mean when spoken by people who speed English on a daily basis. And plenty of well spoken people use “travel as far as” sufficiently well that when one ask “how far did X travel” one can’t always be sure one means “what distance did he cover” rather than “what was the location of his most extreme destination point”.
That said: It’s clear that a student should interpret the question to mean “how far above the launch point did the flowers rise” because otherwise the question cannot be answered. The box doesn’t permit them to enter “this problem is ambiguous” and the kid can be 100% sure the teacher who assigned the problem is not going to give points for any such answer.
lucia,
your squinting is a lot better than mine.
lucia:
Which ultimately is what matters. Whether or not you can tell what that reference point is in some larger context doesn’t change your ability to answer the question so it doesn’t really matter.
It might matter for thought problems people want to do unrelated to the test itself, but for Mark Bofill’s point, that he wouldn’t have even thought about the assumption he would make when reading the question on the test, it’s a non-issue. He wouldn’t have thought about the assumption he was making because the assumption he was making was necessary for the question he was being asked. In other words, he was making an assumption he was supposed to make, so… no big deal.
Brandon,
No one said it was an “issue”. jferguson asked which they meant and I answered. The further discussion revolves around your claim about whether the text itself is clear based on the wording. Our discussing that doesn’t mean anyone thinks that wording is a ‘issue’ with the problem.
lucia:
Huh? Of course nobody said it was an “issue.” I didn’t say anyone did. But I didn’t make a “claim about whether the text itself is clear based on the wording” either. All I did was try to point out to Mark Bofill the assumption he realized he would make without realizing he would make wouldn’t change anything about the problem.
Then you pointed out the question being asked was how far the flowers traveled in relation to the boy’s hand. I agreed that’s what ultimately mattered, not anything else, emphasizing how it meant the assumption Bofill would instinctively make would have no impact on his ability to solve the problem.
I don’t know what your comment is in reference to. You didn’t quote anything, and I can’t find anything in my three comments which make it seem I thought this was an “issue” or that the “text itself is clear based on the wording.”
Ok.. Well, I misunderstood what you intended to communicate when you pointed it out was not an issue. Sorry.
Brandon
I understood ‘Eh. It turns out the boy’s height was irrelevant so the assumption didn’t matter.’
as you suggesting the wording was clear.
The reason I thought so was the combination of two things.
One is the “Eh” (which tends to convey a certain ‘what’s it” as Bertie Woster would say) . The other is your saying the height was ‘irrelevant’ and saying so in context of what had been said previous to your remark.
I’d already pointed out that it would be relevant if we wanted to know the height above the ground. It’s only ‘irrelevant’ if we assume that the question clearly asks for the height above the launch point.
In fact, as far as I can tell, the main reason we conclude the height of the launch point is “irrelevant” is that we can only answer the question asked if we make an assumption to resolve the ambiguity of the question. That assumption is that the text should be read to ask for the height above the launch point and not above the ground.
Everyone used to physics problems is pretty accustomed to making these assumptions.
But anyway, that’s how I understood the combination of “eh” and the rest in context. Turns out that’s not what you meant. That happens.
lucia:
Alright.
For what it’s worth, I was actually meaning the boy’s height was irrelevant because there was no way a boy’s height would come into play when the flowers were traveling 30+ meters and the balcony was only a little over 10 meters high. I was under the impression the question was just a yes/no question of whether or not the flowers would reach the girl, which is why my second comment said:
I was under that impression because when I squinted and looked at the question under the image, I saw the question, “Was that high enough for her to catch the flowers?” Since I saw the post say:
I understood that to mean the question being discussed was simply a yes/no question we had to do physics to determine the answer for. It was only just now I noticed the questions asked before and after the image are actually different, with the student only being asked how high the flowers travel above the image. Presumably, that is the answer expected in the answer box, not “Yes.”
I would have noticed that sooner, but I didn’t squint too much at the picture, taking the post’s description on faith. The difference in understanding that led to may have caused some confusion.
More importantly though, it shows this test question was kind of terrible. The student is asked two different questions then provided an answer box. Which answer are they supposed to provide? I would normally give the answer to the question I was most recently asked, but I’m pretty sure the test wants the more informative answer, which was the answer to the earlier question.
I think it’d be pretty bizarre for a student who read, “Was that high enough for her to catch the flowers?” to answer, “Yes” and be told his answer was wrong because he didn’t answer, “33.4 meters.”
Brandon,
Yep. I can see why you might think that. It’s possible a student might read the final question and think the correct answer was either yes pr no. But I happen to know the real question is the one above the picture not the one after the picture and just above the entry box. (I only know this because I know which answer the student has to provide to “get credit” for a “right answer”. So: totally empirical observation of what is “right”.)
This was homework not a test. Their test is Tuesday. So… who knows?
Yep.I think it’s rather fair to suggest hat would be ridiculous. The final question just before the box is a “yes/no” question. The correct answer to the question just above the box is “yes”.
But I’m not sure how well that argument would go over with the teacher. Sometimes in life– often including school– you realize that you might win a battle by arguing but you can’t really win ‘the war’. Or who knows… maybe a student could win that one. I think they are better off not noticing the question is asked twice and stick with the one above the image. Oddly, that’s the one most students seem to “see”. It’s the one I “saw” first.
Wouldn’t accelerating a bundle of flowers from 0 to 50+ mph while moving only about 2 foot rip the flowers to smithereens?
Steve Ta,
I should think the flowers would not survive the acceleration required. Let’s increase set guys arm length to 1 m.
v^2= 0^2 + 2aL
a~ 25.6^2/(2*1) = 327.68 m/s^2
That’s 33 gs. Humans would certainly not survive this. It’s a bit hard to believe flower petals would survive this.
Baseballs are pretty sturdy. So are cannon balls. So is lead shot. Flowers not so much. This is why one is always safer writing a problem where someone hurls shot, fires a bullet or throws a rock or pebble.
On the other hand, I’ve never tested the structural properties of flower petals under high acceleration. If you have some sort of cannon or sling shot you could try shooting flowers at different rates of acceleration though.
Baseball players are pitching forward. I doubt they could pitch up with that speed.
MikeN–
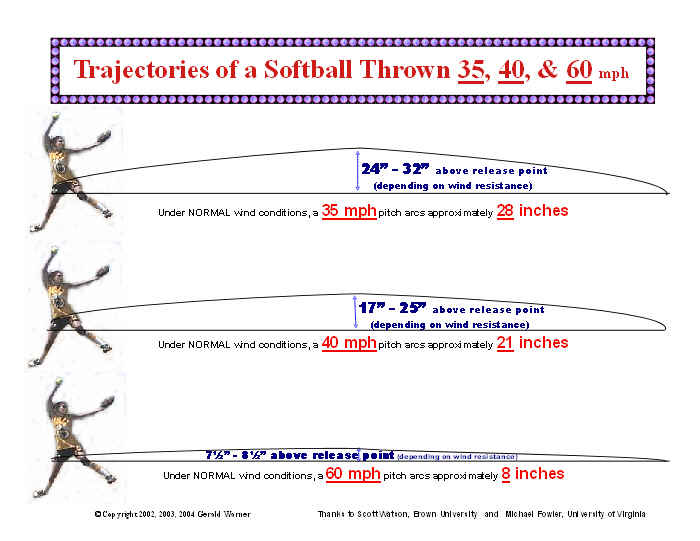
I suspect so as well. I’m pretty sure you can’t throw “up” efficiently over hand. If you want to achieve elevation, you generally throw underhand. High velocities are achieved, but even fast pitch softballs do not achieve a large vertical components:
Does the original author of this question have any inkling that it has engendered such extensive analysis, poor innocent question that it was?
Lucia,
“That’s 33 gs. Humans would certainly not survive this. It’s a bit hard to believe flower petals would survive this.”
.
As with many things, it depends. https://en.wikipedia.org/wiki/G-force
.
John Stapp survived some crazy high g-force tests on a rocket sled; I read about these in the mid 1960’s when I was first starting to learn some mechanics.
SteveF,
I wasn’t aware of the time or direction factors. I just always used rule of thumb. Looks like the one I used is the lower bound… That’s cool– now I know more.
But if the acceleration was uniform at 327 m/s^2 for 1 meter
1 m = 0.5* 327 * t^2
So t= 0.07820619 s.
I remember this one from college, this is the type of question that “brings physics to life”!
1. During World War II the Russians, lacking sufficient parachutes for airborne operations, occasionally dropped soldiers inside bales of hay onto snow. The human body can survive an average pressure on impact of 30 lb/in2 . Suppose that the lead plane drops a dummy bale equal in weight to a loaded one from an altitude of 150 ft, and that the pilot observes that it sinks about 2 ft into the snow. If the weight of an average soldier is 144 lb and his effective area is 5 ft2 , is it safe to drop the men?
Reference https://www.physicsforums.com/threads/parachuting-inside-bales-of-hay.792412/
One would think the forward velocity would be an important consideration. Yet there is no speed given for the plane nor longitudinal effect of the bale entering the snow.
Matt B:
I think my answer would depend on whether or not there would be any practical application of it. Because if there would be, I’d say, “No.” I don’t care what the physics tells me. Nobody is jumping 150 feet out of a plane without a parachute on my say-so, especially not me.
Brandon
I gotta laugh. One of my students had a question about “the light turns yellow… blah.. blah… should she hit the accelerator or the brakes. ” My tendency is to think if you need to hit the accelerator to make the light, you should hit the brakes. That doesn’t mean I always do that. It doesn’t mean others will agree.
Some of these things are value judgements, not physics!
MattB,
Pounds? Inches? Ft? What are those again?
It depends. Is there enough room to stop the car before the intersection without, as we say in racing, standing the car on its nose? Is there someone directly behind you that will hit you if you brake hard? Is cross traffic stopped so no one is going to bust the light at speed and T-bone you in the intersection? Are there any police cars in sight? Is there an automatic camera at this intersection? If you have to think about the answer to any of the above, braking is probably your best choice.
Lucia, sorry about the units, to help calculations please remember:
1 lb = 0.0714 stones
1 ft = 12 in = 0.061 rods
Brandon, you would have been a poor candidate for Hero of the Soviet Union…..but may have lived to go home to Leningrad….which was once Petrograd….which was once St Petersburg……which is now St Petersburg…..which I hope will be Putingrad some day……
I still like speed measured in furlongs/fortnight. I haven’t seen or heard that in quite some time.
1 furlong per fortnight is about 2.976 links per hour. Can’t understand why it’s seldom heard of.
A hay bail is an interesting delivery method. I wonder if that was part of the inspiration behind the successful Rover mission?
https://www.youtube.com/watch?v=KyktvC7w7Js
jferguson (Comment #138894)
John Wheeler reported an exam question by a guy named Cooper. “How far can the wild goose fly?â€
BRIDGEKEEPER: What is the air-speed velocity of an unladen swallow? ARTHUR: What do you mean? An African or European swallow?
Now if the wild goose is metaphysical the answer would simply be, “farther than whatever it is chasing it can go”.
I have a wonderful mental picture of Lucia lobbing sedum into the air. I was always taught that practical testing of any model is essential. I was so impressed that I borrowed some hay bales from the local farmer, chartered a light aircraft and went and found these 3 Russian guys…
… I couldn’t find any snow, so I dropped them onto an open-air ice-rink.
I am in the process of updating my model.
Sort of related: Exam question responses
http://static5.lxdcdn.net/images/max/w/806/419c5563f7ec041aa33ff1026f2ada90.jpeg

Carrick,
Pretty funny. But it’s got to be a spoof all around.
I can’t help but wonder what subject matter was being tested. “What can you never eat for Breakfast?” What’s the right answer? Stones? Hemlock? Uranium?
Unless a teacher taught something in particular looked like half an apple, I’m not sure what that answer is supposed to be either.
Is the answer to “how to lift an elephant” supposed to be “use a lever” Or a pulley?
Lucia, if you google the questions, you’ll see many of the so-called questions are standard riddles. And many of the answers are the standard responses.
So anyway I agree with you they aren’t actually exam questions, just a funny spoof.
I fell into the trap in thinking this was a “yes/no” question. While I calculated the correct numbers and promptly ignored the impossibility of the toss, because of the layout of the question I associated the entry box with the yes/no question immediately above it. If the box accepts “yes” or “no” as an answer, then I would have no feedback showing that I needed to enter the height. And masking “yes” and “no” out of the possible answers is very easy to do.
On another albeit associated topic, and one my son (a HS senior taking AP calculus and physics) is running into routinely is that the computer is looking for a specific answer. In the solution you provide above, if you are strict on the number of significant digits, then there are only two (the acceleration of 9.8 m/s^2) so the answer should be 33 m. The time listed has 3 significant digits (2.61 sec), so if you know that g to 3 digits is 9.81 m/s^2 (and most should), then the answer is 33.4 m. But neither of those are 33.37929 m and the computer will mark both wrong. My son has run into this exact issue time and time again – he does the problem right, but has to spend an inordinate amount of time trying to figure out what number the computer is looking for. He doesn’t mind so much when it’s for homework, but to miss a problem like this on a test is frustrating, and can be damaging!
Dean_1230,
Yep. Depending on the cms used and how the teacher implements it, the computer interface can cause some silliness that amounts to unfairness. Some can be very unfair, and even if not, counter-productive to learning.
Obviously, students shouldn’t be hunting around guessing the number of significant figures the computer is programmed to accept.
When I program Moodle questions, I try to make fairly wide uncertainty ranges. So I try program moodle to accept as right solutions coded using g=10, g=9.8 and g=9.81. (Whether I always succeed… dunno. But that’s my intention. Anyway, using my rule, I’d accept a window at least as wide as 33.4 ± 0.7. Given square-roots and squares, I might make it a bit larger. )
I’d be more persnickety on questions whose intention is to test use of significant figures. But I generally feel that significant figures isn’t something to dwell on when focusing on application of physical concepts. The main student errors tend to be sloppy algebra where they lose ‘±’ signs , not drawing free body diagrams and so on, not understanding that one needs to double time for distance traveled with an ‘echo’ and so on. I don’t want a program to tell a student their otherwise correctly computed answer is “wrong” because it’s off in the 3rd significant digit. If you do that, the test tends to not distinguish between students who have mastered application of concepts and those who have no clue how to do a problem.
Yes, eventually they need to attend to significant figures– lab report write-ups is a good time to do that. But I don’t consider it something to worry about when they are doing their first application of Newton’s laws, kinematics and so on.
(Mind you: I do tell them if their teacher does that, the student should be very careful. I also advise that they need to keep extra sig-figs with intermediate values. Some teachers enforcement of sig-figs is willi-nilly and computer programs tend to make this worse rather than better. In the empirical evidence suggested one teacher around here not-infrequently applies (applied?) the rule of “whatever is the default in Moodle”, which happens to require answers like 12345.xy even if the problem statement only justified 3 significant figures. No one would ever have done that grading by hand, but it’s easy to enter a problem and overlook the need to use something other than the default. When that is habitual by a teacher. I can’t really fix that for the students but yes, it is very frustrating.)
FWIW: The AP uses g=10 m/s^2 in the multiple choice portion. At least AP Phys C does and says so on the front matter. So a teacher who is being strict on significant figures while prepping them for the AP (and likely any test written by the college board) is doing their students something of a dis-service. The college boards view (and fwif the NY Regents ) matches mine: They are not overly concerned with significant figures.
Napoleon didn’t die in battle at all…the others are like the top image here:
http://www.sciencedump.com/content/math-jokes-explained
Carrick,
Oh good. That makes much more sense!
Lucia,
Thanks for your insights. So when using multiple choice tests, how do you determine whether a student understands the concepts or is fighting the computer? For instance, the difference between 9.8 and 10 results in a 0.6 m difference, which is at the outer edge of the acceptable band. Any other rounding error could easily put it over the band. Do you see what they’ve entered and do you make a judgement on whether they understand it? Do you have students provide their worksheets they used to answer the test questions? How do you know how much they know?
A professor once correctly told me that tests are opportunities for the student to learn. Tests show students what they don’t know (a very important thing to know). But without some feedback on where they made their mistakes, how do you impart knowledge back to the student when all they see is that they didn’t get the answer right?
As for 10 m/s, the AP tests use only one significant digit? Wow…
Dean_1230
I think you can never be sure any student tested really understand the concept. But I just can’t believe having problems where the student needs need to pick out answer to “What is the weight of a 10 kg block” and then is challenged to decide between:
100 N, 98 N, 98.1 N and “none of the above” much other than the “student has learned the teachers preferred rounding convention”.
Sure. And sometimes 0.6 m is within the appropriate uncertainty band sometimes it” outside the appropriate uncertainty band. Heck, sometimes 1 km is within the uncertainty band. For this particular problem: the issues associated with drag on flower petals launched at the speeds claimed are sufficient to make claims of greater than 1 significant figure a bit dubious. If that means the uncertainty is greater than 0.6 m, the uncertainty is big. Training students that ‘it must be small’ is a disservice. If it’s big, one should recognize it is big.
Even in problems where drag might be small relative to weight: The acceleration due to gravity on earth actually varies about 0.7% with lower values at the top of mountains and higher values at sea level. Some high school physics problems involve things being dropped from airplanes which could themselves be flying over tall mountains. It’s fair to say that for most high school physics work involving objects on the surface g=9.8 m/s/s is reasonable and that’s a good habit to foster. But anyone who insists on 9.81 m/s/s? One can easily argue they are being unreasonable. And of course, insisting that t=2.61s will magically infuse a problem where g is rounded to 2 significant figures with 3 significant figures is simply incorrect.
Yes. I suspect this is because the college board rightly recognizes diagnosing the number of significant figures from a problem statement is one of the less important things students learn in high school physics. No matter what the problem statement says, to the extent that any problems in high school physics map into the real world, very few problems involve the level of assumptions that result in better than 2 significant figures of accuracy.
One can easily argue that it is better to ensure students understand that using g=10 m/s/s is often just fine and in fact, often the more justifiable choice than keeping 3 or 4 significant figures.
Now: I suspect in chemistry, a fair number of problems do involve a more a larger number of significant figures. One needs to titrate and use some equipment where things are done fairly precisely. But high school physics? The students may be required to record things like mass, time and so on accurately. You want to encourage that. But after they collect their data, you also want them to compare the differences in their results to the actual precision of their set up. If they do so, they ought to understand they aren’t computing anything to 3 significant figures when they do their physics homework– not even if they are really, really, really good, careful, and keep every digit when hitting their calculator buttons.
Dean_1230
To clarify: I tutor students. I do not teach high school classes.
When tutoring I do is create supplemental exercises that help my tutees test whether they have grasped a subject sufficiently to do problems. Some tutees love these, others not so much. (Those who hate them don’t do them. There is a limit to what a private tutor can impose. Basically: you can recommend.)
On the supplemental exercises, I want to make uncertainty bands that are wide enough to deem the answer ‘right’ without having the issue be slight errors in rounding and so on.
But obviously, to achieve my goal I also need the problems to tell them their answer is wrong when they make a conceptual error.
SoI can’t make the window so wide that answers that involved conceptual errors are deemed “right”. Avoiding the latter generally requires thinking about what conceptual errors a student might make and making sure the order of magnitude of competing effects are such that a student making a sign error or losing a 1/2 on a term would result in an answer that is outside the uncertainty range that results from rounding g to 10 and/or making small rounding errors when dealing with intermediate values.
Writing “good” questions requires some thought and I can’t pretend I always manage.
As for tests: With one exception, the students are enrolled in local schools so their teachers assign tests. So those teachers will judge however they judge and I have no power to change those teachers judgements. Even if I am clearly right and the teacher clearly wrong…. no pull here.
That said: If I were grading tests, I would have a ‘free response’ section and I would have students turn those in. I would create a rubric to grade those, and grade them accordingly. When I’ve done it this way, my rubrics tend to emphasize things like “draw a free body diagram”. “Identify correct forces and their directions” and so on with positive points granted for each thing that is done right. Doing all these things correctly strongly correlates with getting the right answer, but generally, if the student merely hits their calculator button wrong, that results in a minor deduction. Meanwhile, if no work is shown but the correct answer magically appears: almost no credit. This is the way I always graded test when I did grade them.
I think the main reason teachers have multiple choice is to permit them to test a broad range of skills while keeping grading time managable. The AP, NY Regents and many teachers present a mix of multiple-choice and free response.
If I had a multiple choice section on a test (and if I taught high school I would) : no I would not have students turn in worksheets to explain their answers on the multiple choice. If I had a “enter into a box on the computer”, also, I would (probably) not have them turn in sheets. For the multiple choice section: The student checks the right box or they don’t. Students who are sloppy with their calculators can easily lose lots of points.
I think at the highschool level, a mix of (properly written) multiple-choice and free response would result in sufficient punishment for kids who are sloppy but know concepts while still allowing them to get some points for mastering concepts.